Machine Learning Method Bayesian Classification

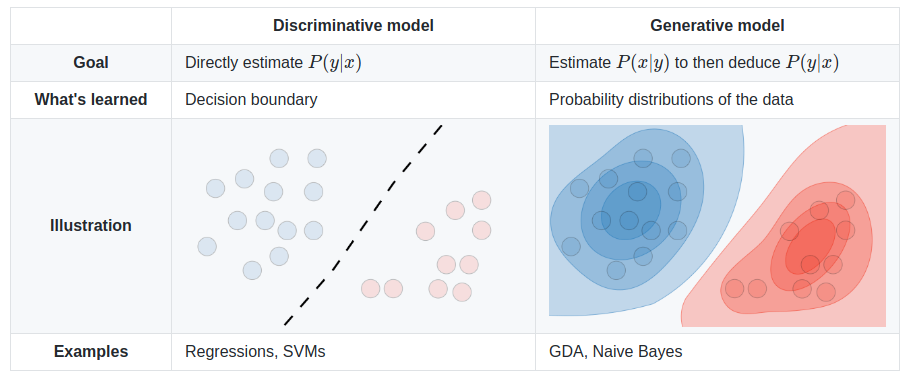
Bayesian classification is a generative model which works best when the data are clustered into areas of highest probibilty. When the data is distributed, but still has a clear bountry, SVM or Regression may do better.

Bayes Theorem expresses the probability that a test prediction will be correct. That seems simple, but there is actually a lot to it. We have some event or state which really happens. Some people get cancer, some emails are spam, etc... and those things happen with some probability. On average, 40% of us will get cancer at some point in our lives and at any given time, about 1% of the population is currently battling cancer. More than half of all email is spam. Some percentage of your tomato plants are getting too much water.

Then, we can apply a test (or tests) to an individual to help detect that state. If the test shows a positive result, now we know the chances are higher... but how much higher? The test could be wrong (a False Positive) and we need to know how often that happens. Doctors keep track of how often a test flags a patient for cancer vs how often the patient actually turns out to have cancer. You (and your spam filter) keep track of how often an important email is placed in your junk box.

If you get a cancer screening test, and it is positive, and that test is 90% accurate, does that mean you have a 90% chance of having cancer? No, because only 1% of the people actually have cancer right now, so the 10% error rate of the test is 10% of the 99% who are healthy. Your chances are actually 90% of the 1% with cancer divided by the 10% of the 99% who are healthy or about 0.9%/9.9% = ~9%. So your risk went from 1% to 9%. Not good, but a cancer screening test with only a 90% accuracy rate wouldn't be very useful. This is related to true positives and false positives, accuracy vs precision and recall.

For any case where we make a decision based on a prediction, we might right or wrong in deciding one way or the other. We might say "Yes" and be right (true positive) or be wrong (false positive). Or say "No" and be right (true negative) or wrong (false negative). If we make a chart of the possibilities, it might look like this:

In mathematical terms, Bayes Theorem says:

P(A|X) = ( P(X|A) * P(A) ) / P(X)

Where:

• P(A) is "how often the answer is yes overall". In the table above, this is True Positives + False Negatives / all cases. In other words, all the outcomes in the Actual Answer = Yes column divided by all the outcomes. How many people have cancer right now? How many emails are spam?
   
• P(X) means "the probability that we will predict yes with our test". This is True Positives + False Positives / all cases or all the outcomes in the Predicted Answer = Yes row divided by all the outcomes. How often does our screening test scare the crap out of a patient? How often do emails go into the spam folder?
  Keep in mind, that in reality, there may be many different X's; many different tests. The probability of each test must be looked at individually. So perhaps our test is "does this email have the word 'dollars' in it?" and we are trying to predict if it's a spam email. There might be another test that asks if there is a reference to a product we often purchase, or a site we frequent, or perhaps a reference to a pill we don't take. These tests work together, but each is true a different percentage of the time.
   
• P(X|A) means the probability that this test actually triggers when the answer is true. The "|" can be pronounced "given" so "the probability of X given A." This is the "True Positive" in the box above / all cases. How many people had cancer, and had this indicator which is detected in the test? How many emails had this word in it?
   
• P(A|X) means "the probability that our prediction, X, matches the actual answer, A.". "probability of A given X". If the test is positive, this is the probability that the answer is actually "Yes".

So how does that help us? Let's take a common example of spam filtering. We could express this as:

P(spam|word) = ( P(word|spam) * P(spam) ) / P(word)

Now, if we have a set of emails, where the user has marked the spam as spam, and we pick out one word, let's use "dollar", and made a note of which emails that word appears in, well, we have everything on the right side.

• P(word) is the number of emails containing the world "dollar" / total emails
• P(spam) is the number of spam emails / total emails
• P(word|spam) or in this case P("dollar"|spam) is the number of emails with the word dollar which were marked as spam

Putting all those numbers into the right side, gives us the percentage association of the word "dollar" with a spam email; the likelihood that an email is spam if it has "dollar" in it. So if we are given a new email, we can compute the probability that it is spam simply by looking to see if the word "dollar" appears in it, and if it does, this email is P(spam|"dollar") likely to be spam. Of course we need to track more than just one word, but the nice thing about probabilities is that they just multiply together.

In Python using Naive Bayes from SciKit-Learn.org:

import sys
from time import time
import numpy
from sklearn.naive_bayes import GaussianNB

### Load features_train, labels_train as numpy arrays of features and lables.
### Make features_test, labels_test as subsets of the training data for testing.

classifier =  GaussianNB()

t0 = time()
fit = classifier.fit(features_train, labels_train)
print "training time:", round(time()-t0, 3), "s"

t0 = time()
prediction = classifier.predict(features_test)
print "prediction time:", round(time()-t0, 3), "s"
print prediction

score = classifier.score(features_test,labels_test)
print score

See also:

• http://scikit-learn.org/stable/modules/naive_bayes.html Libraries, examples, etc...
• https://www.burakkanber.com/blog/machine-learning-naive-bayes-1/ Explination and code in Javascript
• http://shiffman.net/teaching/a2z/analysis/#bayes
• http://statpages.info/#Bayesian lots of fun online interactive Bayes things.
• https://medium.freecodecamp.org/logistic-regression-the-good-parts-55efa68e11df

Questions:

• It is, however, easy to misuse.
  +

  .