 Gaussian
(Normal) Distribution
Gaussian
(Normal) Distribution
 Gaussian
(Normal) Distribution
Gaussian
(Normal) Distribution
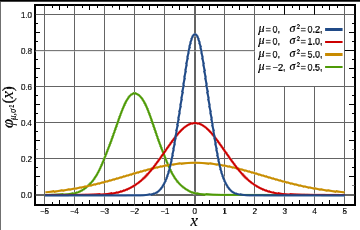
If the probability distribution of X is Gaussian^ (aka Normal) with mean (µ or mu) and variance sigma squared (ó2 or sigma2) we write X ~ N(µ, ó2). {ed, using ó as the greek letter sigma}. µ gives us the center of the normal bell curve, ó is the standard deviation^ or width from the center of the curve to the inflection point^ where the slope of the curve changes from concave to convex. ó2 is the variance.
In the figure here, the red line is the Normal distribution.
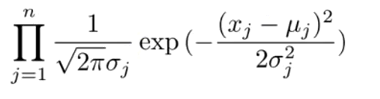
Another way of calculating this is:
ó2=o^2
a = 1/sqrt(2 * Pi * ó2)
g(x) = a * exp(-0.5 * ( (x-µ)^2 / ó2) )
Where ó2 is the variance which controls the width of the peak, µ is the "expected value" or position of the center of the peak, and a is the height of the peak. Setting a to 1/sqrt(2* Pi * ó2) makes the integral of the curve exactly 1, so the area under the curve is a single unit.
Gausian functions are often used as kernels in Support Vector Machines, or in Anomaly Detection. They are also used in Kalman Filters for localization
See also:
| file: /Techref/method/math/gaussian.htm, 2KB, , updated: 2017/6/29 17:11, local time: 2025/6/15 13:37,
216.73.216.159,10-2-252-0:LOG IN
|
| ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions? <A HREF="http://www.sxlist.com/techref/method/math/gaussian.htm"> Math Methods for Gaussian Distribution</A> |
| Did you find what you needed? |
Welcome to sxlist.com!sales, advertizing, & kind contributors just like you! Please don't rip/copy (here's why Copies of the site on CD are available at minimal cost. |
|
The Backwoods Guide to Computer Lingo |
.