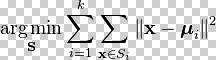 So K-Means is
minimizing
sum(||x(i)-µ(k)||2)/m
So K-Means is
minimizing
sum(||x(i)-µ(k)||2)/m
Given data with no labels (e.g. only X data, no y) find clusters in that data.
Pick some number of points that you want to cluster your data into. Randomly set those "centroid" points to locations in the data space. Assign each datapoint to the centroid closest to it. Move the centroid to the center of the points assigned to it. Repeat.
In Octave:
%SETUP
M = size(X,1);
%K < M (because we are grouping the data into fewer clusters
Kmax = floor(M/2); %no point if less than 2 points in each
costold = inf; % start with infinite cost.
%The µ centroids can be set to random datapoints
µr = randperm(M); % Makes a list from 1:M in random order
for K = 1:Kmax % slowly increase K
% assign K cluster centroids µ1, µ2, ... µK,
µ = X(µr(1:K), :); %Picks out first K of those values from X
% Assign points to local cluster and return cost
[C,cost] = groupCentriods(X, µ);
if (cost < costmax) break; endif
if (abs(cost - costold) < costelbow) break; endif
costold = cost;
endfor
%K-MEANS
%Repeat { % How many times?
% Assign points to local cluster around centroids
[C,cost] = groupCentriods(X, µ);
% Move cluster centroids to center of clusters data points
µ = moveCentroids(X, C, K);
} % and that's how you do the K-Means!
function [C,cost] = groupCentriods(X, µ)
for i = 1:M % for every datapoint
% find C(i) := index (1:K) of cluster centroid closest to x(i)
dmin = inf; % start with infinite distance
for k = 1:K % look at every cluster centroid
d = sum( (X(i,:)-µ(k,:)).^2 ); % find distance
if d < dmin % if this centroid is closer
C(i) = k; % record its number
dmin = d; % remember how close we got
endif
endfor
%Faster replacement for the inner (for k) loop:
% d = µ - repmat(X(i,:),M,1);
% [dmin C(i)] = min(sum(d .^ 2,2));
cost = cost + dmin; % accumulate the cost
endfor
end
function µ = moveCentroids(X, C, K)
for k = 1:K % for every cluster
% µk := mean position of points assigned to cluster k
p = [,]; % start a list of points nearest this cluster
for i = 1:M % for every datapoint
if (C(i) == k) % if this point was assigned to this cluster
p = [p; X(i,:)]; % save it
endif
endfor
if length(p) > 0
µ(k,:) = mean(p); % move centroid to middle of cluster
else % no data points near cluster?
µ(k,:) = x(rand * M,:); % move to a new random position
% could also delete
endif
%Faster (assuming there are no empty clusters):
% p = find(C == k); %p is an array of indexes here
% u(k,:) = mean(X(p,:));
endfor
end
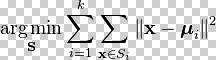 So K-Means is
minimizing
sum(||x(i)-µ(k)||2)/m
So K-Means is
minimizing
sum(||x(i)-µ(k)||2)/m
Choosing K: Choosing the number of clusters, K, can be difficult to automate.
Elbow Method: We can try to run the method multiple times with increasing numbers for K and perhaps find a point where the final cost has dropped rapidly and then stops decreasing much as K increases. This is called the elbow method, and works well if there are very obvious clusters. In other cases, it can be very difficult to find any point where the cost decreases is significantly less.
Maximum Allowed Error Method: Another way is to increase K until the cost (maximum error in the cluster) is below some pre-set value.
Avoid Local Clusters: The clusters may come out differently depending on their initial positions. In cases with a small number of K, (less than 100, certainly less than 10) then the centroids may get stuck in local clusters and not do a good job of finding larger clusters. To avoid this, try multiple random initializations and test each without moving the centroids to find the one that generates the lowest cost.
Equal Sized Clusters: K-Means tends to find clusters that are the same size. In a dataset with a clusters that are larger or smaller, this can lead to poor clustering. Expectation Maximization or EM Clustering ^avoids this.
See also:
| file: /Techref/method/ai/Clustering.htm, 5KB, , updated: 2015/8/28 15:25, local time: 2025/7/1 10:03,
216.73.216.215,10-1-90-29:LOG IN
|
| ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions? <A HREF="http://www.sxlist.com/techref/method/ai/Clustering.htm"> Machine Learning Method Clustering</A> |
| Did you find what you needed? |
Welcome to sxlist.com!sales, advertizing, & kind contributors just like you! Please don't rip/copy (here's why Copies of the site on CD are available at minimal cost. |
Welcome to www.sxlist.com! |
.