
- Write a truth table expressing the outputs
 and
and  as a
function of
as a
function of 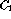 ,
,  and
and 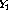 .
.
- Write an algebraic statement in Boolean algebra describing this truth table.
- Implement this statement using standard (AND, OR, EX-OR and inverter gates).
- Make a truth table for A, B, C and Q, where Q is true only when an odd number of bits are true in the number.
- Write a statement in Boolean algebra for Q.
- Convert this equation to one that can be mechanized using only two XOR gates. Draw the resulting circuit.
- Write a truth table for this function.
- Using boolean algebra, write an expression indicating when Q is true. Your statement should include one logical statement for each of the six true conditions, each separated by the OR function. Therefore this statement should utilize a number of AND/NAND functions, and five OR statements.
- Simplify this statement so that it can be implemented using two
two-input AND gates, one OR gate, one exclusive OR gate and one
logical inverter. The expression has the form
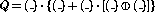 , where
, where 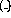 stands for any of the four input signals or their logical
inverses.
stands for any of the four input signals or their logical
inverses.
- Implement this simplified function using logic gates.